Half wave rectifier query

 This is my answer to SE EE question Half wave rectifier query.

My answer

Seeing the forest behind the trees

After these comprehensive but specific answers, I will try to summarize what has been done and why it has been done in this way (ie, I will try to guess what were the intentions of the author when they assembled the circuit). My personal belief is that without this concluding "philosophical" part, we cannot claim to have understood the circuit... and this is true of any such situation when we are trying to understand an unknown circuit. As they say, we must see not only the "trees" but also the "forest" behind them.

Initial observations

OP: "In the circuit, we can see 3 differentiated parts: One half-wave rectifier, one envelope detector and a comparator."

Really, we can see a rectifier in this circuit but it is not only precise but also a full wave rectifier. It seems the latter was more important for the author, because the accuracy of the rectifier is largely made meaningless by the second diode… and this has been noticed by the OP:

OP: "I still don't get why you need this precision rectifier when you already rectify the signal with the envelope detector."

Exactly! If the author was only interested in precision, they would make the elegant circuit of a "non-inverting peak detector" including the second diode in the feedback loop of an op-amp.

So somehow a full-wave precision rectifier is made; let's see how...

How a full-wave precision rectifier is made

What we see is a half-wave precision rectifier made by an op-amp inverting amplifier with a diode included in the feedback loop. Let's consider its operation with the hope to see how it acts as a full-wave rectifier.

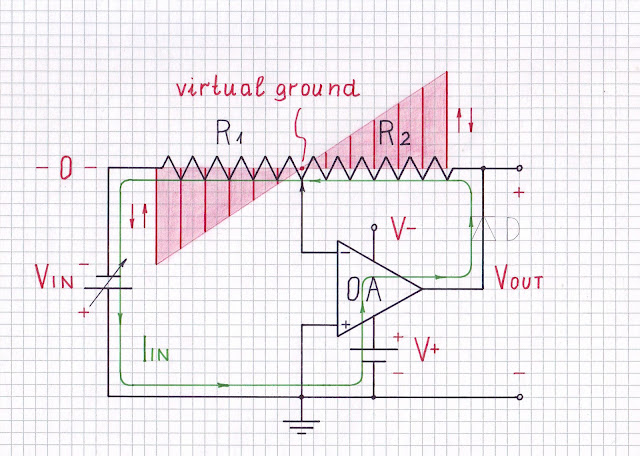
I suggest to show in a more attractive way the circuit operation by visualizing the voltage distribution inside the resistors (along their resistive film). I call this picture "voltage diagram" (I have considered in detail this visualization technique in one of my Codidact papers and also in my Wikibooks story about Ohm's experiment). For this purpose, imagine the two resistors in series as a linear potentiometer with two partial resistances R1 and R2 .

For convenience, the voltage diagram is superimposed on the resistors (the zero voltage level of the ground is lifted to the resistors).

If you prefer, you can imagine the circuit operation at an even lower level - through the mechanical lever analogy.

In addition to the voltage diagram, I have shown were currents flow by current loops (I have considered this visualization technique in another of my Codidact papers). Note something very important - to close the current paths, I have connected the voltage sources.

Elements that do not perform any function and are not important for the explanations are only hinted in pale gray.

Unloaded half-wave rectifier

Let's first consider the circuit operation when there is no load connected (open circuit).

Negative half wave. During the negative half wave of the input voltage, the voltage of the virtual ground begins decreasing. To restore it, the op-amp begins increasing (by the help of the positive power supply V+) its output voltage until it neutralizes the voltage drop across the forward-biased diode (only 0.7 V) and across the resistor R2. Note something interesting - all the circuit elements (both voltage sources, both resistors and the diode) are connected in a loop and the same current flows through them.

Since the output voltage is taken after the diode, the latter seems to have disappeared and the circuit acts as an ordinary inverting ampifier with K = -1. The negative input half wave is inverted and appears as positive at the output.

In the mechanical lever analogy, we can imagine that, for example, you lower the left resistor's (lever) end while I lift the right resistor's (lever) end so that the middle point does not move.

Positive half wave. During the positive half wave of the input voltage, the voltage of the virtual ground begins increasing. To restore it, the op-amp begins decreasing (by the help of the negative power supply V-) its output voltage almost up to V- with the hope to zero the virtual ground… but to its great surprise it encounters unexpected resistance from the diode which is off:-) and fails reaching the negative rail.

Now something is happening that, at first, seems very unpleasant to us - the virtual ground is no longer a ground, and imagine the whole input voltage appears at the circuit output! As you can see from the voltage diagram, since there is no current flowing through the resistors, there are no voltage drops across them and all the points along the resistive film inside resistors have the same (input) voltage.

In the mechanical lever analogy, we can imagine that, for example, you lift the left resistor's (lever) end and the whole resistor (lever) is raised while remaining parallel to itself.

Our instinctive desire is to solve this "problem" by somehow closing the feedback, for example by a second diode connected in the opposite direction between the op-amp output and its inverting input. But if we do so, we will miss the chance to invent an original full-wave rectifier circuit...

And here we come up with the idea "to make lemonade from lemon" - instead of destroying the "bad" voltage, let's use it as an output voltage during the positive input half-wave. What a great idea!

Thus the full-wave output signal is "assembled" by two half waves: the first is a mirror copy of the negative input half wave and it is created by the op-amp with the help of V+; the second follows the positive input half wave.

Loaded half-wave rectifier

Now let's see how our "creation" behaves when it is loaded.

Negative half wave. There is no change compared to the same picture above because, notice, the load is powered by the positive power supply and not by the input source.

Positive half wave. Unfortunately, now a real problem appears since the load is powered by the input source through the resistors R1 and R2. The voltage diagram shows how the local voltages gradually decrease and the output voltage across the load is reduced.

Assembling a full-wave rectifier

The remedy is obvious - inserting an op-amp follower (buffer) between the circuit output and the load. This is how we get to the OP's circuit...

Inventing a new circuit solution

Since we already have another op-amp, we can just put the second diode inside its feedback to obtain a precision peak detector! Now we have two cascaded precision circuits - a full-wave precision rectifier and a precision peak detector; we have obtained both precision and "full-waveness"...

Here is how, creatively thinking, we made a little invention...

Formulating new principles of inventing

It is a good idea to summarize the ideas derived from the invention of this specific circuit solution as inventive principles so that we can use them in solving other circuit problems. We can give them descriptive figurative names.

Inventive principle 1: Transferring voltage through high resistance.

We can see it, for example, in transistor amplifier stages and logic gates when the transistor is off... in bootstrapped circuits or in some exotic op-amp circuits like instrumentation amplifier (see my Codidact paper).

Inventive principle 2: Neutralizing undesired elements by putting them into the negative feedback loop.

In both op-amp stages considered here we can find the same idea - we can destroy the "disturbing elements" (diodes, resistors, etc.) creating an undesired voltage drop, resistance, etc. by inserting them into the negative feedback loop. The op-amp will compensate the undesired voltage drop by increasing its output voltage with the same value... and the voltage after the disturbing element will be not affected; so we can use it as an output voltage.

Seeing the principles in life

We can see the first principle, for example, in the electrical circuits of our lives when we detect the presence of voltage after high-resistance loads... or when measuring the voltage of a "bad" voltage source without load (open circuit)... or maybe, in some mechanical arrangements.

The second principle is even more universal so we can see it all around us. All living things (including us), when implementing their goals, compensate for losses by adding equivalent income...