"Изобретяване" на базови схеми с операционни усилватели

За мен беше голямо предизвикателство да покажа основната идея на транзисторните усилвателни стъпала, като ги изграждам и преоткривам стъпка по стъпка. Но още по-голямо предизвикателство е да се покаже идеята зад по-сложните усилвателни стъпала, реализирани с операционни усилватели: неинвертиращ усилвател, инвертиращ усилвател, диференциален усилвател и накрая измервателен усилвател. Ще го направя тук по същия изобретателски начин, като ги изграждам стъпка по стъпка и разкривам идеята зад тях. Аз използвам този подход в часовете си по "Специализирана компютърна електроника" (СКЕ) от 2004 г. и Полупроводникови елементи" (ПЕ) от 2015 г. Публикувал съм и статия What is the idea behind the op-amp instrumentation amplifier? в секция Electriacal Engineering на уеб платформата за въпроси и отговори Codidact.

Построяваме схемите

Ще започнем от най-простите усилателни схеми с единичен (несиметричен) вход и ще стигнем до изящната схема на измервателния усилвател. Ето моя "построителен сценарий"...

Стъпка1: Несиметрични усилватели

Това са схеми на повторители (K = 1) и инвертори (K = -1) с отрицателна обратна връзка. За да ги накараме да усилват, прилагаме хитър трик - включваме затихване във веригата на обратната им връзка. В стремежа си да го компенсират, те се превръщат в усилватели. Ето и конкретните реализации, в които реализираме затихването чрез делител на напрежение.

1. Неинвертиращ усилвател.

2. Инвертиращ усилвател.

Стъпка 2: Несъвършен диференциален усилвател

Но, както при транзисторните реализации, в много случаи ние се нуждаем от схеми с две входни напрежения, които усилват разликата между тях (така наречените диференциални усилватели). Така, че нека да се опитаме да намерим втори вход с противоположно действие на първия във всяка от горните две реализации. Имаме две възможности да направим това:

1. В схемата на неинвертиращия усилвател, можем да вмъкнем втория входен източник между левия край на входния резистор R и масата. Така получаваме още един вход, но той е инвертиращ:

2. В схемата на инвертиращия усилвател, можем да вмъкнем втория входен източник между неинвертиращия вход и масата. Така получаваме още един вход, но сега той е неинвертиращ:

В резултат на това, получаваме същата диференциална схема.

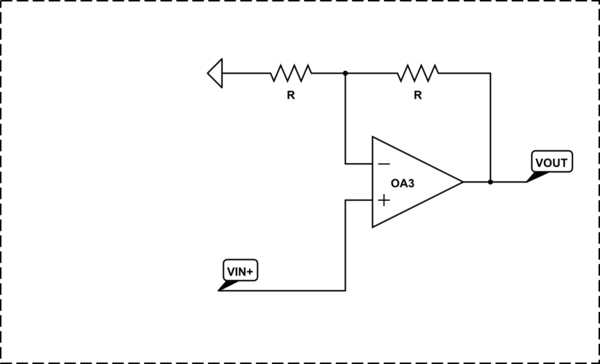
Стъпка 3: Обикновен "диференциален усилвател"

Но тук възниква проблем - коефициентът на усилване на неинвертиращия вход е с единица по-голям от коефициента на усилване на инвертиращия вход (интересно е да се обясни защо). Започваме да търсим начин как да изравним коефициентите на усилване на двата входа. Имаме две възможности:

1. Можем да намалим усилването на неинвертиращия вход с единица с помощта на делител на напрежение. Така получаваме класическата 4-резисторна схема на простия диференциален усилвател:

2. Можем да увеличим усилването на инвертиращия вход с единица чрез допълнителен неинвертиращ усилвател:

На времето, те са избрали първото решение по очевидни причини - не само, защото то е красиво и симетрично:-), но просто защото операционните усилватели са били скъпи. Нека да проследим това решение...

Стъпка 4: Подобрен диференциален усилвател

Но 4-резисторната схема има съществен недостатък - ниско входно съпротивление (в допълнение, то е различно за двата входа). Лошото е, че разликата вмежду вътрешните съпротивления на входните източници разбалансира схемата.

Първата мисъл, която ни хрумва, за да решим проблема, е разбира се, да включим повторители на напрежение преди входовете:

Това разрешава проблема с входното съпротивление... но нов проблем възниква, ако се нуждаем от значително усилване - възможностите на второто стъпало да усилва са ограничени и трябва да накараме входното стъпало също да усилва.

Сръпка 5: Прототип на измервателен усилвател

Очевидното решение е да накараме входните повторители на напрежение да усилват, т.е. да ги превърнем в неинвертиращи усилватели като вмъкнем делители на напрежение между изходите и инвертиращите входове на усилвателите.

Обаче възниква нов проблем - синфазното усилване. Просто казано, ние искаме входното стъпало да усилва входните напрежения, когато те се изменят в противоположна посока и в една и съща степен, и да не усилва, когато те се изменят в същата посока. Това означава, че средната точка между двата резистора Rg/2 не трябва да бъде постоянна маса: в първия случай, тя трябва да е "неподвижна", а във втория случай тя трябва да е "подвижна". Как да го направим това?

Стъпка 6: Измервателен усилвател

Знаменитата транзисторна диференциална двойка, наричана фигуративно "дългоопашата двойка" (long-tailed pair), може да ни помогне. Следвайки тази силна идея, просто "откачаме" долните резистори Rg/2 от масата и ги обединяваме в един общ резистор Rg = Rg/2 + Rg/2. Така веригата от трите последователно свързани резистора се оказва "закачена" между изходите на двата операционни усилвателя (това е същата резистивна сумираща схема като веригата R1-R2 в един инвертиращ усилвател).

Изследваме действието на схемата

То може лесно да бъде визуализирано по един атрактивен начин като покажем разпределението на потенциалите вътре в резисторите (по резистивния слой). Аз наричам тази картина "потенциална диаграма" (разгледал съм подробно тази визуализираща техника в статията си What are voltages inside resistors? в уеб платформата Codidact и в историята Walking along the Resistive Film в Wikibooks). Можете да си представяте трите резистора като един линеен потенциометър с два плъзгача.

Потенциалната диаграма може да бъде допълнена от картина на токовете (разгледал съм подробно тази визуализираща техника в друга статията си Where do currents flow in circuits? в  Codidact, но тук, за простота, не съм изплзвал тази техника). Накратко, ще протича ток през резистивната верига, ако има разлика между изходните напрежения на операционните усилватели. Той ще излиза от изхода с по-високо напрежение и ще влиза в изхода с по-ниското напрежение.

Схемата има различно поведение (работи в различни режими) в зависимост от това как променяме входните напрежения.

Диференциален режим

Нека първо да разгледаме най-простия случай, когато сме приложили две еднакви по стойност, но различни по полярност напрежения (VIN- and VIN+) на входовете. Това означава, че диференциалният усилвател работи в "чист" диференциален режим (без синфазно напрежение).

Когато напреженията се изменят в противоположна посока с една и съща "скорост", така наречената виртуална маса (точка с нулев потенциал) се появява в средната точка вътре в резистора Rg (сякаш тя е свързана с масата). Двата неинвертиращи усилвателя не са истински замасени; те са виртуално замасени. Започваме да разбираме, че това е значителна разлика, защото те ще си взаимодействат през общата точка... и това ни напомня за транзисторния диференциален усилвател, където два транзистора си взаимодействат по подобен начин.

Най-добрият начин да разберем и обясним интуитивно схемите с отрицателна обратна връзка е да разглеждаме операционния усилвател не като едно пропорционално (безинерционно), а по-скоро като интегрално (бавно) устройство... т.е. като някакво мързеливо "същество", което непрекъснато наблюдава напрежението на входа си и изменя напрежението на изхода си. Така, че като изменят изходното си напрежение, операционните усилватели в тази схема се опитват да направят напрежението на инвертиращия си вход равно на напрежението на неинвертиращия вход.

Образно казано, те "дърпат" през резисторите R, както в играта "теглене на въже", общата средна точка към себе си - когато OA1 я "дърпа" нагоре, OA2 я "дърпа" надолу и обратно. Или представете си веригата от трите последователно свързани резистора като "прът" (двустранен лост), който операционните усилватели повдигат или спускат в двата края в обратна посока един спрямо друг. В резултат на това, средната точка не "помръдва"... нейното напрежение стои неизменно равно на нула. Можете да "видите" тази вълшебна виртуална маса, ако отворите Rg и докоснете резистивния слой със сондата на волтметъра.

Процесите в тази "сдвоена" схема не са толкова прости, както в един инвертиращ усилвател, защото има две системи с отрицателна обратна връзка, които си взаимодействат. В този режим те се "борят" помежду си да променят напрежението на средната точка. Усилването е максимално, защото входните стъпала действат като неинвертиращи усилватели (същите като тези по-горе).

В допълнение към този "напълно диференциален режим", където едновременно променяме двете входни напрежения, има два по-прости режима, където меним само едно напрежение, а другото го поддържаме постоянно. В тези случаи виртуалната маса няма да стои само вътре в Rg, а ще се мести и появява вътре в резисторите R.

Синфазен режим

В "чистия" синфазен режим, покаьан на фигурата по-долу, двете входни напрежения стоят равни, когато ги изменяме в една и съща посока с една и съща "скорост". Така напреженията на двата входа на операционните усилватели, всички точки вътре в резистивната верига (включвайки Rg с неговата средна точка) и двата изхода на операционните усилватели, се изменят по един и същи начин. Просто казано, всички точки на входната верига са еквипотенциални. В резултат на това, входните стъпала действат като повторители на напрежение.

Образно казано, операционните усилватели "дърпат" общата средна точка... или местят краищата на "лоста"... но сега в една и съща посока.

Забележете, че ток не тече през резисторната верига, понеже двата операционни усилвателя имат еднакви изходни напрежения и няма напрежителна разлика върху веригата.

Отново има две системи с отрицателна обратна връзка, които си взаимодействат, но в този случай те си "помагат" една на друга в стремежа си да променят напрежението на средната точка.

Диференциален и синфазен режим

В практиката, двата режима съществуват едновременно. Нека да разгледаме по-простия случай, когато двата входни сигнала се променят диференциално спрямо един синфазен сигнал (две еднакви входни напрежения).

Този режим е много подобен на "напълно диференциалния режим" по-горе. Единствената разлика е, че напрежението на средната точка между резисторите Rg/2 не е нула, а е само постоянно (виртуалната маса е изместена нагоре до нивото на синфазното напрежение.

Можете да разгледате "живи" потенциални диаграми на тези режими в този филм, който съм качил в Google Photos. Компютъризирания експеримент, показан там, съм описал подробно в Walking along the Resistive Film.

Действието на схемата може да се визуализира като се покажат какви са напрежителните падове върху резисторите и къде текат токовете (виж моя отговор на въпрос в платформата StackExchange). Там съм демонстрирал обратния подход за разкриване на базовата идея - чрез разграждане на схемата стъпка по стъпка (reverse engineering).

Базовата идея

Търсейки основната идея в това красиво симетрично схемно решение, можем да я видим в двойственото поведение на средната точка вътре в резистора Rg: от една страна, при диференциалния режим, тя има фиксирано напрежение; от друга страна, при синфазен режим, това напрежение следва измененията на входните напрежения. Образно казано, при диференциалния режим то е "твърдо" и "неподвижно", докато при синфазния режим то е "меко" и "подвижно".

Уеб ресурси

Investigating basic op-amp amplifier circuits - същата история в блога ми, но на английски език

What is the idea behind the op-amp instrumentation amplifier? - подобна моя статия, публикувана в секцията Electrical Engineering на платформата за въпроси и отговори Codidact