The Secret of Invention: Invention in Action
This is the seventh (last) article in the series The Secret of Invention, published in the popular Bulgarian magazine Young Designer in 1984. In it, I have illustrated the basic principles of invention through examples from my inventive practice.
Invention in Action
Now it is time to illustrate the application of some of the basic principles of invention. The proposed ideas are selected from my own inventive experience and are interesting in that they reveal the "technology" of invention. Therefore, do not be surprised if some of them seem unreal, fantastic, and others turn out to be already known.
In previous materials, we have repeatedly pointed out that in order to successfully generate new ideas, a certain mental attitude of consciousness is necessary. It occurs under certain conditions and is characterized by raising self-esteem, optimism and desire to work. As a student, for me these moments occurred during a session. This is not accidental. During the academic semester, the student's duties are multiple - lectures, exercises, tests, protocols, etc. and they hardly have time left to dream (more precisely, there is time, but it is fragmented). When a session comes, all obligations, except for one - to take the exam, fall away. At the same time, you are left alone with yourself and, willy-nilly, you have to push yourself to understand some things. Then the questions arise.
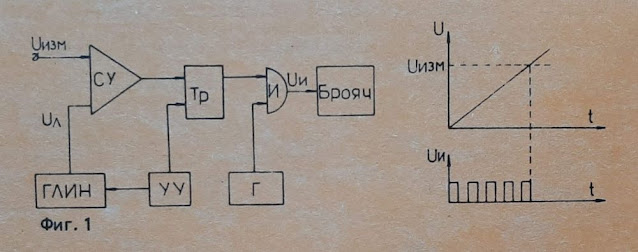
So, one evening I was studying another question - an analog-to-digital converter with the conversion of the voltage into a time interval and filling it with reference pulses. Its operation principle is known (Fig. 1).
The control device УУ periodically starts a ramp generator ГЛИН, which is compared with the measurement voltage Uизм by a comparison device (comparator СУ). At the same time, the trigger Тр is established and pulses enter the counter from the reference generator Г through the valve И. When the linearly varying voltage becomes equal to the measurement, the comparator resets the trigger and pulses no longer pass through the valve. The content of the counter is proportional to the voltage measurement value.
Perhaps the word itself directed my attention to a process that is characterized by a natural stoppage as a result of some losses. After overcoming the mental inertia of thinking and it became clear that the pulses do not necessarily have a rectangular shape and the same amplitude, the moment of insight came - as a measuring element to use an oscillating system with a high quality factor (ie with small losses), in which free damping oscillations Y are excited by the measured signal X and counted (Fig. 2). And immediately an idea came to me for a device that can measure the amplitude of a voltage pulse in digital form (Fig. 3). It contains only one quartz resonator КР, comparing device СУ (comparator) and counter Бр. The voltage pulse acts on the quartz crystal, deforming it. After the pulse disappears, the resonator performs damping mechanical oscillations, and corresponding electrical oscillations appear on its electrodes, which are fed to the comparator. At its output, a bunch of rectangular pulses is obtained, which are counted by the counter.
Interestingly, the number of pulses depends logarithmically on the amplitude of the signal, which allows it to be read in logarithmic units (for example, decibels). So the device implements the functions of an analog-to-digital logarithmic converter in the simplest possible way (the classical way of such conversion is implemented with complex electronic circuits).
Quite naturally, the next question arises: "Why should not a mechanical resonator be excited directly by a mechanical impact?" Imagine that you are holding a tuning fork in your hand. You hit it lightly with a hard object and it starts to sound, gradually decreasing in volume until it disappears completely. With a stronger impact, the sound will last longer. If, with a suitable device, you count the oscillations from the start of the impact until their complete attenuation, you will get information about the strength of the impact in digital form. Thus, another interesting application of the method was obtained - a device for measuring the amplitude of mechanical shocks.
So far, it has been assumed that the resonator has a high and constant quality factor, and the variable quantity is the amplitude of the excitation effect (voltage pulse, mechanical shock, etc.). Having accepted that the reverse is performed (the resonator is excited by pulses of constant amplitude, and the variable quantity is the quality factor) - the "upside down" method, I came up with the idea of measuring quantities that affect the quality factor in this way. So, for example, the quality factor of the tuning fork depends on the viscosity (density) of the medium in which it vibrates (i.e., the same force of impact will result in a different number of oscillations depending on the medium in which the tuning fork is located - air , water, oil, etc.). So, the next application of the method was a "digital reading viscometer".
A chance idea, which I figuratively called "the tuning fork principle", took hold of me more and more. I felt that this turned out to be a golden nugget and I started frantically looking for other applications as well. The results came after I looked at this process in a slightly different way. I reasoned like this:
"There is a resonator in front of us. It "responds" to a suitable impact by generating damped oscillations with a precisely defined frequency. Therefore, the resonator can act as a secret key. Here is one of the most interesting applications of the "tuning principle" - recognition of objects from a distance. As is known, this is necessary at checkpoints (recognition and release of "yours", but stopping of "foreign ones"), alarm systems, etc. For this purpose, the object (for example, a person) is supplied with LC - flickering circuit (parallel-connected coil and capacitor pressed into a plastic plate), which plays the role of a key (Fig. 4). A transmitter is installed in the transmission point, which periodically emits powerful electromagnetic pulses (method of periodic action) and a receiver. The pulses are induced in the coil of the oscillating circle and excite in it free damping oscillations of a strictly defined frequency.They are radiated back from the oscillating circle and perceived by at the receptacle. According to their frequency, it can be determined who is passing ("own" or "foreign"). This application perfectly illustrates the method of periodic action - the transmitter emits a pulse ("question"), and in the pause the LC-oscillating circuit "answers" (I called the method "question-answer").
Later it occurred to me: "Couldn't the LC-circuit be controllable?" For example, with one switch K (fig. 5) to turn it on and off as desired. Then it becomes a passive transmitter, with which, for example, a teller can signal unnoticed in an attempted bank robbery. What if the capacitance of the capacitor or the inductance of the coil were made dependent on some quantity X (temperature, pressure, etc.)? A non-contact converter of the type "quantity X - frequency" is obtained. In this way, you can get information about temperature, acidity, pressure, etc. into a person's digestive system if they swallow a tiny tube-pill beforehand.
Many interesting ideas were obtained after I applied the "tuning principle" to volume resonators. Imagine, for example, a flat piezo element-reflector ПЕ, against which a strictly parallel flat reflector О is located (Fig. 6). If the piezo element emits a short pulse, it will reflect many times before it dies out. The frequency of the received pulses at the output of the piezo element is proportional to the distance l - we get a "displacement-frequency" converter.
Up to this point we have assumed that the medium between the two reflectors is stationary. And if it is movable? For example, we have immersed the reflectors in running water. As the fluid (in this case water) moves, the ultrasonic pulse describes a "harmonic" that stretches in proportion to the speed of the fluid (Fig. 7). The number of multiple reflections decreases because some of them are "blown" by the fluid outside the area of the two reflectors. So, we got a "speed - number of pulses" converter, i.e. ultrasonic flow meter with digital reading.
To clarify the processes in recent applications, I used various analogies. For example, I imagined the reflectors to be two parallel walls between which a ping-pong ball (ie the ultrasound pulse) bounces - a direct analogy. It was clear that if the wind blew, the ball would move not only perpendicularly, but also parallel to the walls. Or I imagined that the receivers were the banks of a river in which I (ie, the ultrasonic pulse) was swimming perpendicular to the current of the river, as "again" from one bank to the other - a personal analogy. And in this case, it becomes clear that I am swimming along a "harmonica" trajectory, which stretches in proportion to the speed of the current.
-------------
That's it, using all weapons to fight against routine thinking - emotional "pumping", suppression of criticism and self-criticism, "figurative" thinking, analogies, "squeezing" the random phenomena, with frequent transfers from one field of technique to another, new ideas are "generated". Some of them will turn out to be useless, others - minor, and some... maybe they will change the course of history. Try it!
(The end)
Eng. Cyril Mechkov
Comments
Post a Comment