В предишната си история ви разказах как с моите студенти превърнахме един реален волтметър в "идеален". Сега ще ви разкажа как след това направихме същото с един реален амперметър.

Компенсационен метод за измерване на ток

ПРЕДПОСТАВКИ ЗА ВЪЗНИКВАНЕ

ВОЛТМЕТЪР. Основен проблем на измервателната техника е, че реалните измервателни уреди оказват въздействие върху измерваната стойност - те я променят и показват променената стойност. Така например, в предишната история наблюдавахме как реалният волтметър отклонява (изважда) част от тока, протичащ през измерваната верига, и в резултат на това, измерваното напрежение намалява. Като включихме втори източник с еквивалентно, но противопосочно на измерваното напрежение, ние "спряхме" тока, протичащ през волтметъра и така го превърнахме в "идеален". След това заменихме ръчно-управлявания източник с операционен усилвател и стигнахме до заключението, че по този начин са изградени схемите с последователна отрицателна обратна връзка (неинвертиращите схеми с операционни усилватели като повторител на напрежение, неинвертиращ усилвател и др.)

АМПЕРМЕТЪР. Реалният амперметър пък въвежда (изважда) пад на напрежението и в резултат на това, измерваният ток намалява. Сега изниква въпросът "Как да направим идеален амперметър? Не можем ли да приложим подобен трик с включване на допълнителен източник?" В тази история ще покажа, че това е възможно и този "трик" стои в основата на схемите с паралелна отрицателна обратна връзка (инвертиращите схеми с операционни усилватели като преобразувателя ток-напрежение, инвертиращия усилвател и др.)

ИСТОРИЯ. Интересно е, че двете схеми на "идеални" измервателни уреди не са изобретени едновременно - първо се появява "идеалният" волтметър, а доста по-късно и "идеалният" амперметър. Защо това е така? Вероятно, защото през 19 век е имало добри амперметри (магнитоелектрически галванометри с ниско съпротивление), но е нямало добри (с високо съпротивление) волтметри. Те са нямали волтметър и е трябвало да го направят чрез амперметър и последователно свързан резистор с относително ниско съпротивление (действащ като преобразувател напрежение-ток). По-късно се появяват много добри електронни волтметри (аналогово-цифрови преобразуватели), но пък е нямало електронни амперметри. И е трябвало да направят амперметър, като свържат резистор с относително високо съпротивление (действащ като преобразувател ток-напрежение) успоредно на волтметъра.

НАСТОЯЩЕ. Тази фундаментална идея (наричана още „виртуална маса“) стои в основата на съвременните схеми с паралелна отрицателна обратна връзка, реализирани с операционни усилватели (типични представители са преобразувателят ток-напрежение и инвертиращият усилвател). Нека тогава да я експериментираме така, както го направихме и със схемата на "идеалния" волтметър - като построяваме стъпка по стъпка опитната постановка. Това ще ни помогне да осъзнаем общата базова идея, която стои зад всичките тези устройства. Ето един възможен “сценарий”, който осъществих през пролетта на 2022 г. с моите студенти.

РЕАЛИЗАЦИЯ НА МЕТОДА

1. Сглобяваме измерваната схема. Нека да изследваме възможно най-простата електрическа верига (Фиг. 1а), в която източник на напрежение V = 12 V захранва резистор със съпротивление R = 10 k. В резултат на това, протича ток I = V/R = 12/10 = 1,2 mA (съгласно закона на Ом).

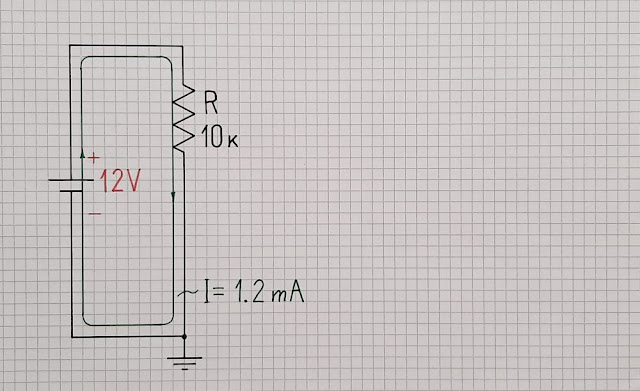Фиг. 1а. Възможно най-проста електрическа верига - източник на напрежение захранва резистор.

За да наблюдаваме едно видимо въздействие на несъвършенния амперметър върху измерваната верига, сме избрали съпротивлението на резистора да е сравнително ниско - 10 k. По-късно изкуствено ще увеличим съпротивлението на амперметъра, като добавим последователно резистор с още по-ниско съпротивление 1 k - Фиг. 1б.

Фиг. 1б. Постоянни резистори със сравнително ниско съпротивление - 10 k и 1 k.

Амперметрите, с които разполагаме в лабораторията, са цифрови мултицети DT830B (Фиг. 1в). На обхват 2 mA, който смятаме да използваме тук, те имат входно съпротивление 100 ома (измерихме го на едно от предишните лабораторни упражнения).

Фиг. 1в. Амперметрите в лаб. 1217 са цифрови мултицети DT830B.

Те са снабдени със специални миниатюрни накрайници (сонди), с които можем удобно да ги включваме в контактните гнезда на платката (виж по-долу) - Фиг. 1г.

Фиг. 1г. Волтметрите включваме в гнездата на платката чрез миниатюрни „сонди“.

Елементите ще монтираме върху експериментална платка за монтаж на елементи без запояване – Фиг. 1д. Тя се състои от множество "разклонителни точки" (групи от по пет контактни гнезда, наредени в къси вертикални линии) и "шини" (групи от по пет разклонителни точки, наредени в дълги хоризонтални линии в горната и долна част на платката).

Фиг. 1д. Експериментална платка за монтаж на елементи без запояване.

Връзките между елементите ще правим със съединителни проводничета (джъмпери) с различна дължина и цвят – Фиг. 1е.

Фиг. 1е. Проводничета за свързване на елементи върху експерименталната платка.

Нека да захраним тази най-проста схема с „идеален“ източник на положително напрежение (адаптор 12V/1A) – Фиг. 1ж. По-късно ще добавим и същия източник на отрицателно напрежение. Понеже източниците са "плаващи" (незаземени), ще използваме едни и същи адаптори, но с разменени изводи.

Фиг. 1ж. „Идеални“ източници на напрежение (адаптори 12V/1A).

Фиг. 1з. Схемата, монтирана на платката и захранена с +12 V…

Фиг. 1... и в едър план.

2. Измерваме тока с „лош“ амперметър. Теоретично, токът във веригата би трябвало да бъде 1,2 mA. Когато обаче разкъсаме веригата и включим нашия амперметър със сравнително голямото си съпротивление от 100 ома (Фиг. 2), то се добавя към съпротивлението на резистора. Общото съпротивление става 10,1 k и токът намалява - I = V/(R + RA) = 12/10,1 = 1.18 mA. Казано по друг начин, върху съпротивлението на амперметъра възниква напрежителен пад VA = I.RA = 118 мV и токът намалява - I = (V - VA)/R = (12 - 0.118)/10 = 1.18 mA.

Фиг. 2а. Измерваме тока с „лош“ амперметър (100 ома съпротивление).

Фиг. 2б… монтирано на платката…

Фиг. 2в… показано в едър план.

Може би ви прави впечатление, че амперметърът на Фиг. 2б показва 1,2 mA, а не 1,18 mA. Това е така, защото адапторът дава малко по-високо от 12 V напрежение - някъде около 12,18 V (виж Фиг. 1з). Но за простота, нека приемем, че напрежението му е точно 12 V.

Нека да измерим с волтметър пада на напрежение върху амперметъра - Фиг. 2г.

Фиг. 2г. Измерваме пада на напрежение върху амперметъра.

Фиг. 2д. … показан в едър план.

И така, включването на реалния амперметър във веригата е равносилно на включването на резистор 100 ома последователно на резистора R – Фиг. 2е.

Фиг. 2е. Реалният амперметър е еквивалентен на резистор със съпротивление 100 ома...

Получава се парадокс, както беше и при реалния волтметър: Когато не сме включили амперметъра, токът във веригата е точно, колкото трябва да бъде; включим ли амперметъра, той „поврежда тока“ и показва „повредената“ стойност!

3. Включваме компенсиращ източник. Щом като проблемът е в това, че се губи напрежителен пад върху амперметъра, трябва да намерим начин да компенсираме този пад. Очевидно, трябва да прибавим същото напрежение и тогава резултатът ще бъде нулев напрежителен пад (липса на загуби) върху този участък от веригата. На практика това означава да включим един втори "подпомагащ" източник на напрежение, последователно и еднопосочно на основния източник – Фиг. 3. Двете напрежения ще се сумират и резултатното напрежение на този съставен източник ще стане 12,12 V.

Фиг. 3. Компенсираме напрежителния пад върху амперметъра чрез втори източник със същото напрежение.

Забележете, че двете напрежения са с противоположна полярност спрямо масата. Но те са еднопосочни, когато обхождаме контура, и затова се сумират. Накратко, те са противопосочни по отношение на масата, но са еднопосочни вътре в контура.

4. Реализираме компенсиращия източник. Както вече знаем от предишната история, най-простият начин да получим регулируемо отрицателно напрежение е с помощта на потенциометър, захранван от втори източник с отрицателно напрежение 12 V – Фиг. 4а. Той не е много добър източник на напрежение, но в нашия случай това няма особено значение, защото ще настройваме неговото напрежение до постигане на равенство (принцип на отрицателната обратна връзка).

Фиг. 4а. Реализираме компенсиращия източник чрез потенциометър, захранен с второ отрицателно напрежение 12 V.

Използваме любимия ни от предишния и множество други експерименти линеен потенциометър със съпротивление 1 к – Фиг. 4б. Неговите три извода са разположени на стандартното за интегралните схеми разстояние; затова можем удобно да го монтираме на експерименталната платка. Трябваше само да усучем изводите му на 90 градуса, за да контактува надеждно в гнездата.

Фиг. 4б. Използваме линеен потенциометър със съпротивление 1 к...

Фиг. 4в… монтиран на платката…

Фиг. 4г. … показан в едър план.

5. Настройваме компенсиращото напрежение. За да направим това напрежение точно равно на напрежителния пад върху амперметъра, включваме един чувствителен волтметър (на обхват 200 mV) като нулев индикатор, така че той да отчита резултатното напрежение върху веригата от двата последователно включени елемента (амперметър и потенциометър)... и го настройваме така, че да покаже нулево напрежение (така наречената "виртуална маса") - Фиг. 5а.

Фиг. 5а. Включваме нулев индикатор…

Фиг. 5б… монтиран на платката…

Фиг. 5в. … показан в едър план.

За да постигнем максимална точност, действаме по следния начин: Първоначално избираме по-груб обхват на волтметъра (типично 20 V) и уравновесяваме схемата. След това го намаляваме и отново уравновесяваме схемата... и така, докато достигнем до най-малкия обхват на волтметъра (200 mV за нашия уред).

В резултат на тези действия, веригата от последователно свързаните амперметър и компенсиращ източник (потенциометър, захранен от източник на отрицателно напрежение 12 V) се държи като късо съединение... "парче проводник" с нулево съпротивление... все едно, че имаме схемата от Фиг. 1и пред нас. В резултат на това, токът се определя само от входното напрежение 12 V и съпротивлението на резистора R = 10 k (I = V/R = 12/10 = 1,2 mA).

6. Възлагаме работата на операционен усилвател. Настройването на компенсиращото напрежение равно на входното напрежение е досадна рутинна работа. Затова решаваме да я възложим на един операционен усилвател. Така получаваме класическата схема на един усъвършенстван чрез операционен усилвател амперметър - Фиг. 6а.

Фиг. 6а. Заменяме потенциометъра с операционен усилвател…

Фиг. 6б. „Добрият стар 741“ ще свърши добра работа.

Разбира се, днес има много по-съвършени от 741 операционни усилватели, но тук ние не преследваме особена точност. Целта ни е да разберем идеята, принципа... Поради това няма сега да задълбаваме в грешките на операционните усилватели. Те са достатъчно добри за нашите цели...

Фиг. 6в. Монтираме схемата на платката…

Сега остава да начертаем нашата схема по традиционния начин – Фиг. 6г. Означаваме общата точка на резистора, амперметъра и инвертиращия вход с термина "виртуална маса" и така я правим по-лесна за разпознаване от конвенционално мислещите хора.

Фиг. 6г. Конвенционално начертана схема на "идеален" амперметър.

7. Опростяваме максимално схемата. Още повече бихме могли да опростим схемата, ако премахнем захранващите изводи на операционния усилвател, захранващия източник и изтрием токовите контури - Фиг. 7. Но къде остава разбирането на смисъла от всичко това?

Фиг. 7. Максимално опростена схема на "идеален" амперметър.

ДОПЪЛНИТЕЛНИ ЕКСПЕРИМЕНТИ

8. Изкуствено „влошен“ амперметър. Сега можем да включваме всевъзможни „лоши“ амперметри, но показанието им ще бъде едно и също (вярното), защото операционният усилвател ще ги подпомага в съответната степен. Проблемът е, че амперметрите ни са сравнително добри (т.е., съпротивлението им не е достатъчно голямо) и падът на напрежение върху тях е много малък (стотици миливолти)... а ние имаме нужда от „лоши“, за да покажем ефективността на тази идея. Ако искаме да направим пада по-забележим, можем изкуствено да увеличим съпротивлението на амперметъра, като добавим последователно резистор с доста по-голямо съпротивление, например 1 k - Фиг. 8a. Ако резисторът е променлив, можем да меним степента на „влошаване“ и да го направим колкото си искаме „лош“.

Фиг. 8а. Влошаваме умишлено амперметъра като изкуствено увеличаваме съпротивлението му.

Фиг. 8б. Монтирано на платката (в едър план).

9. Наблюдаваме напрежението на компенсиращия източник. Интересно е да наблюдаваме "огледалното копие" на напрежителния пад върху амперметъра (т.е., напрежението на компенсиращия източник). За целта нека да включим един волтметър паралелно на несъвършенния амперметър и друг - паралелно на компенсиращия източник (изхода на потенциометъра) - Фиг. 9а. Така ще можем да наблюдаваме едновременно вредния напрежителен пад върху амперметъра и "огледалното" отрицателно напрежение на операционния усилвател, което го компенсира.

Фиг. 9а. Включваме волтметри към амперметъра и компенсиращия източник.

Виждаме, че компенсиращото напрежение в случая на изкуствено "влошен" амперметър (R = 1,1 к) е много по-високо (1,32 V, Фиг. 6а) отколкото напрежението (120 mV) в случая на оригиналния волтметър (R = 100 ома). А не можем ли да използваме това напрежение за нещо полезно?

10. Използваме напрежението на компенсиращия източник. Така достигаме до идеята да направим един "идеален" преобразувател ток-напрежение (transimpedance amplifier), който да включим на входа на аналогово-цифров преобразувател - Фиг. 10а. Получаваме един съвременен "идеален" амперметър.